（本小题满分12分）如图，在矩形ABCD中AB="1," BC=
, 点P为矩形ABCD所
在平面外一点，PA⊥平面ABCD，点E为PA的中点。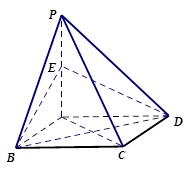
（Ⅰ）求证：PC//平面BED；
（Ⅱ）求直线BD与平面PAB所成的角的大小.
相关试题
的定义域为[0，1]且同时满足：①对任意
②
③若
的值；
的前n项和为Sn，且
，
是以q为公比的等比数列（q为常数）
的通项公式；
是等比数列，半求
的通项公式；
处的切线方程为
，求a的值；
对任意
都成立，求实数x的范围。
的图象与x轴的交点中，相邻两个交点之间的距离为
，且图象上一个最高点
的解析式；
的前6项和为60，且
的等比中项
满足：
，求数列推荐套卷
（本小题满分12分）如图，在矩形ABCD中AB="1," BC=, 点P为矩形ABCD所
在平面外一点，PA⊥平面ABCD，点E为PA的中点。
（Ⅰ）求证：PC//平面BED；
（Ⅱ）求直线BD与平面PAB所成的角的大小.
粤公网安备 44130202000953号