如图示，已知平行四边形ABCD和矩形ACEF所在平面互相垂直，AB=1，AD=2，
是线段EF的中点．
（1）求证：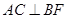
；
（2）设二面角A—FD—B的大小为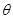
，求
的值；
（3）设点P为一动点，若点P从M出发，沿棱按照
的路线运动到点C，求这一过程中形成的三棱锥P—BFD的体积的最小值．
相关试题
，当
时，有
，解关于x的不等式
。
是R上的偶函数,且当
时,函数的解析式为
的值;
时,函数的解析式;
上是减函数;
的终边上有一点P（
，m），且
m，
与
的值。
的集合；
的图象经过怎样的变化而得到的。
为第三象限角，
．
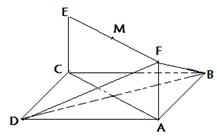
，求推荐套卷
如图示，已知平行四边形ABCD和矩形ACEF所在平面互相垂直，AB=1，AD=2，是线段EF的中点．
（1）求证：；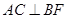
（2）设二面角A—FD—B的大小为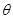，求的值；
（3）设点P为一动点，若点P从M出发，沿棱按照的路线运动到点C，求这一过程中形成的三棱锥P—BFD的体积的最小值．
粤公网安备 44130202000953号