已知抛物线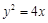 ,点
,点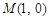 关于
关于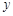 轴的对称点为
轴的对称点为 ,直线
,直线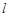 过点
过点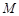 交抛物线于
交抛物线于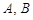 两点.
两点.
(1)证明:直线 的斜率互为相反数;
的斜率互为相反数;
(2)求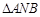 面积的最小值;
面积的最小值;
(3)当点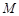 的坐标为
的坐标为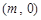 ,
, 且
且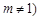 .根据(1)(2)推测并回答下列问题(不必说明理由):
.根据(1)(2)推测并回答下列问题(不必说明理由):
①直线 的斜率是否互为相反数? ②
的斜率是否互为相反数? ②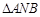 面积的最小值是多少?
面积的最小值是多少?
推荐套卷
已知抛物线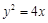 ,点
,点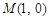 关于
关于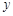 轴的对称点为
轴的对称点为 ,直线
,直线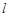 过点
过点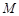 交抛物线于
交抛物线于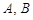 两点.
两点.
(1)证明:直线 的斜率互为相反数;
的斜率互为相反数;
(2)求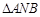 面积的最小值;
面积的最小值;
(3)当点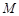 的坐标为
的坐标为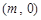 ,
, 且
且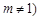 .根据(1)(2)推测并回答下列问题(不必说明理由):
.根据(1)(2)推测并回答下列问题(不必说明理由):
①直线 的斜率是否互为相反数? ②
的斜率是否互为相反数? ②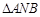 面积的最小值是多少?
面积的最小值是多少?