已知A、B、C是直线l上不同的三点,O是l外一点,向量 满足:
满足: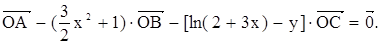 记y=f(x).
记y=f(x).
(1)求函数y=f(x)的解析式:
(2)若对任意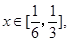 不等式|a-lnx|-ln[f'(x)-3x]>0恒成立,求实数a的取值范围:
不等式|a-lnx|-ln[f'(x)-3x]>0恒成立,求实数a的取值范围:
(3)若关于x的方程f(x)=2x+b在[0,1]上恰有两个不同的实根,求实数b的取值范围.
推荐套卷
已知A、B、C是直线l上不同的三点,O是l外一点,向量 满足:
满足: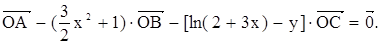 记y=f(x).
记y=f(x).
(1)求函数y=f(x)的解析式:
(2)若对任意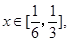 不等式|a-lnx|-ln[f'(x)-3x]>0恒成立,求实数a的取值范围:
不等式|a-lnx|-ln[f'(x)-3x]>0恒成立,求实数a的取值范围:
(3)若关于x的方程f(x)=2x+b在[0,1]上恰有两个不同的实根,求实数b的取值范围.