如图，在由小正方形组成的12×10的网格中，点O、M和四边形ABCD的顶点都在格点上．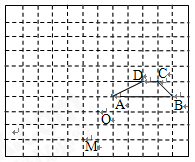
（1）画出与四边形ABCD关于直线CD对称的图形；
（2）平移四边形ABCD，使其顶点B与点M重合，画出平移后的图形；
（3）把四边形ABCD绕点O逆时针旋转90°，画出旋转后的图形．
相关试题
如图，在由小正方形组成的12×10的网格中，点O、M和四边形ABCD的顶点都在格点上．（1）画出与四边形ABCD关于直线CD对称的图形；
（2）平移四边形ABCD，使其顶点B与点M重合，画出平移后的图形；
（3）把四边形ABCD绕点O逆时针旋转90°，画出旋转后的图形．
－1）2＝0，问单项式3x2ym＋n－1和 x2m－n＋1y4是同类项吗？
粤公网安备 44130202000953号