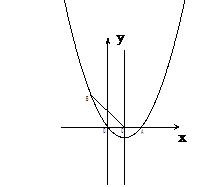如图,已知抛物线经过点B(-2,3)、原点O和x轴上另一点A,它的对称轴与x轴交于点C(2,0),求此抛物线的函数关系式;
联结CB, 在抛物线的对称轴上找一点E,使得CB=CE,求点E的坐标;
在(2)的条件下, 联结BE,设BE的中点为G,在抛物线的对称轴上是否存在点P,使得△PBG的周长最小?若存在,求出P点坐标;若不存在,请说明理由.
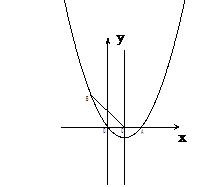
相关知识点
推荐套卷
如图,已知抛物线经过点B(-2,3)、原点O和x轴上另一点A,它的对称轴与x轴交于点C(2,0),求此抛物线的函数关系式;
联结CB, 在抛物线的对称轴上找一点E,使得CB=CE,求点E的坐标;
在(2)的条件下, 联结BE,设BE的中点为G,在抛物线的对称轴上是否存在点P,使得△PBG的周长最小?若存在,求出P点坐标;若不存在,请说明理由.