盒中装有
个零件，其中
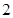个是使用过的，另外
个未经使用.
（Ⅰ）从盒中每次随机抽取
个零件，每次观察后都将零件放回盒中，求
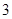次抽取中恰有次
抽到使用过的零件的概率；
（Ⅱ）从盒中随机抽取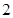个零件，使用后放回盒中，求此时盒中使用过的零件个数为3或4概率。
.
相关试题
（
）
时，求经过原点且与圆
相切的直线
的方程；
内切，求实数
的值.
＋ln x(a≠0，a∈R)．求函数f(x)的极值和单调区间．
经过点
.
，求直线
通过不同三点
，且直线
斜率为
,
是
轴上的动点，
分别切圆
两点，
恒过一定点;
的最小值.
，
（
），函数
，且
图象上一个最高点为
，与
.
为常数，判断方程
在区间
上的解的个数；
中，若
，求
的取值范围.推荐套卷
盒中装有个零件，其中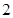个是使用过的，另外个未经使用.
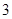（Ⅰ）从盒中每次随机抽取个零件，每次观察后都将零件放回盒中，求次抽取中恰有次
抽到使用过的零件的概率；
（Ⅱ）从盒中随机抽取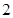个零件，使用后放回盒中，求此时盒中使用过的零件个数为3或4概率。
.
粤公网安备 44130202000953号