(本小题满分14分)
已知函数f(x)=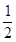 x
x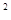 -ax + (a-1)
-ax + (a-1)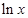 ,
,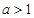 .
.
(I)讨论函数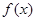 的单调性;
的单调性;
(II)若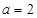 ,数列
,数列 满足
满足 .
.
(1) 若首项 ,证明数列
,证明数列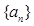 为递增数列;
为递增数列;
(2) 若首项为正整数,数列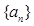 递增,求首项的最小值.
递增,求首项的最小值.
相关知识点
推荐套卷
(本小题满分14分)
已知函数f(x)=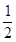 x
x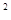 -ax + (a-1)
-ax + (a-1)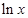 ,
,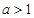 .
.
(I)讨论函数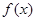 的单调性;
的单调性;
(II)若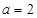 ,数列
,数列 满足
满足 .
.
(1) 若首项 ,证明数列
,证明数列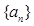 为递增数列;
为递增数列;
(2) 若首项为正整数,数列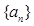 递增,求首项的最小值.
递增,求首项的最小值.