(本小题满分14分)做一个体积为32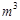
,高为2
的长方体纸盒.
(1)若用
表示长方体底面一边的长,
表示长方体的表面积,试写出关于的函数关系式;
(2)当取什么值时,做一个这样的长方体纸盒用纸最少?最少用纸多少
?
的定义域为
，且
时，
时，
．
，解答下述问题：
的取值范围；
，求实数
，集合
．
时，求
；
，求实数
的取值范围；
，求实数
；
，集合
，集合
；
，求实数
的取值范围；推荐套卷
(本小题满分14分)做一个体积为3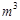2,高为2的长方体纸盒.
(1)若用表示长方体底面一边的长,表示长方体的表面积,试写出关于的函数关系式;
(2)当取什么值时,做一个这样的长方体纸盒用纸最少?最少用纸多少?
粤公网安备 44130202000953号