有粮食和石油两种物资，可用轮船与飞机两种方式运输，每天每艘轮船和每架飞机的运输效果见表．
 |
轮船运输量／ |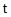
飞机运输量／ |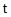
| 粮食 |
 |
 |
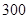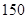| 石油 |
 |
 |
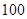现在要在一天内运输至少
粮食和
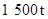石油，需至少安排多少艘轮船和多少架飞机？
相关试题
.
的最小正周期；
上的最大值与最小值.
中，角
的对边分别为
，已知
.
的值；
，求
和
的值.
，其中
.
，求曲线
在点
处的切线方程；
有三个零点，求
的取值范围.
，且
.
；
.
，其中
.
时判断
的单调性；
在其定义域为增函数，求正实数
的取值范围；
，当
时，若
，总有
成立，求实数
的取值范围.推荐套卷
有粮食和石油两种物资，可用轮船与飞机两种方式运输，每天每艘轮船和每架飞机的运输效果见表．
|
轮船运输量／ |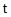
飞机运输量／ |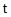
| 粮食 |
|
|
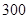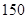| 石油 |
|
|
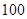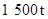现在要在一天内运输至少粮食和石油，需至少安排多少艘轮船和多少架飞机？
粤公网安备 44130202000953号