某高校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作. 规定:至少正确完成其中2题的便可提交通过.已知6道备选题中考生甲有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都是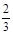 ,且每题正确完成与否互不影响. 求:
,且每题正确完成与否互不影响. 求:
(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(2) 试从两位考生正确完成题数的数学期望及至少正确完成2题的概率分析比较两位考生的实验操作能力。
相关知识点
推荐套卷
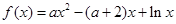 ,其中
,其中 .
.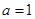 时,求曲线
时,求曲线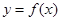 的点
的点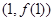 处的切线方程;
处的切线方程;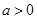 时,若
时,若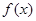 在区间
在区间 上的最小值为-2,求
上的最小值为-2,求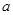 的取值范围;
的取值范围; ,且
,且 恒成立,求
恒成立,求 的焦点为
的焦点为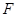 ,
, 为
为 上异于原点的任意一点,过点
上异于原点的任意一点,过点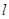 交
交 ,交
,交 轴的正半轴于点
轴的正半轴于点 ,且有
,且有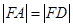 ,当点
,当点 为正三角形.
为正三角形. ,且
,且 和C有且只有一个公共点E.
和C有且只有一个公共点E.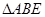 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.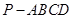 中,底面
中,底面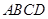 为矩形,
为矩形,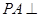 平面
平面 为
为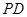 的中点.
的中点.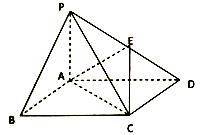
 平面
平面 ;
;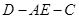 为60°,
为60°,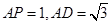 ,求三棱锥
,求三棱锥 的体积.
的体积. 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为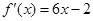 ,数列
,数列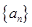 的前n项和为
的前n项和为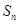 ,点
,点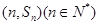 均在函数
均在函数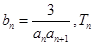 是数列
是数列 的前n项和,求使得
的前n项和,求使得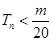 对所有
对所有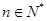 都成立的最小正整数
都成立的最小正整数 .
. 中,
中, 、
、 、
、 分别为角
分别为角 、
、 、
、 所对的边,且角
所对的边,且角
 的值;
的值; 时,求
时,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号