甲打靶射击,有4发子弹,其中有一发是空弹(“空弹”即只有弹体没有弹头的子弹).
(1)如果甲只射击 次,求在这一枪出现空弹的概率;
次,求在这一枪出现空弹的概率;
(2)如果甲共射击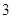 次,求在这三枪中出现空弹的概率;
次,求在这三枪中出现空弹的概率;
(3)如果在靶上画一个边长为 的等边
的等边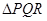 ,甲射手用实弹瞄准了三角形
,甲射手用实弹瞄准了三角形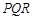 区域随机射击,且弹孔都落在三角形
区域随机射击,且弹孔都落在三角形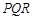 内。求弹孔与
内。求弹孔与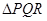 三个顶点的距离都大于1的概率(忽略弹孔大小).
三个顶点的距离都大于1的概率(忽略弹孔大小).
推荐套卷
甲打靶射击,有4发子弹,其中有一发是空弹(“空弹”即只有弹体没有弹头的子弹).
(1)如果甲只射击 次,求在这一枪出现空弹的概率;
次,求在这一枪出现空弹的概率;
(2)如果甲共射击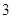 次,求在这三枪中出现空弹的概率;
次,求在这三枪中出现空弹的概率;
(3)如果在靶上画一个边长为 的等边
的等边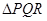 ,甲射手用实弹瞄准了三角形
,甲射手用实弹瞄准了三角形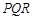 区域随机射击,且弹孔都落在三角形
区域随机射击,且弹孔都落在三角形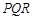 内。求弹孔与
内。求弹孔与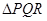 三个顶点的距离都大于1的概率(忽略弹孔大小).
三个顶点的距离都大于1的概率(忽略弹孔大小).