在平面直角坐标系中,一动点P( ,y)从M(1,0)出发,沿由A(-1,1),B(-1,-1),C(1,-1),D(1,1)四点组成的正方形边线(如图①)按一定方向运动。图②是P点运动的路程s(个单位)与运动时间
,y)从M(1,0)出发,沿由A(-1,1),B(-1,-1),C(1,-1),D(1,1)四点组成的正方形边线(如图①)按一定方向运动。图②是P点运动的路程s(个单位)与运动时间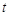 (秒)之间的函数图象,图③是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.
(秒)之间的函数图象,图③是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.
(1)求s与
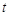 之间的函数关系式。
之间的函数关系式。(2)求与图③相对应的P点的运动路径;及P点出发多少秒首次到达点B;
(3)写出当3≤s≤8时,y与s之间的函数关系式,并在图③中补全函数图象.
相关知识点
推荐套卷
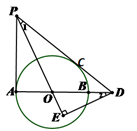
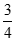 ,求OE的长。
,求OE的长。 的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端
的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端 的仰角为35°,朝着这棵树的方向走到台阶下的点C处,测得树顶端
的仰角为35°,朝着这棵树的方向走到台阶下的点C处,测得树顶端 ,台阶AC的坡度为
,台阶AC的坡度为 (即
(即 ),且
),且 、
、 、
、 三点在同一条直线上.请根据以上条件求出树DE的高度(参考数据:tan65°
三点在同一条直线上.请根据以上条件求出树DE的高度(参考数据:tan65° 2.1,cos65°
2.1,cos65° 1.7,结果保留一位小数).
1.7,结果保留一位小数).
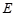 、
、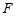 是
是 、
、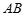 的中点,
的中点,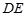 、
、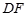 的延长线分别交
的延长线分别交 的延长线于
的延长线于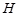 、
、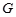 ;
;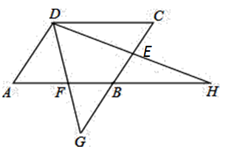
 为菱形,试判断
为菱形,试判断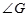 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.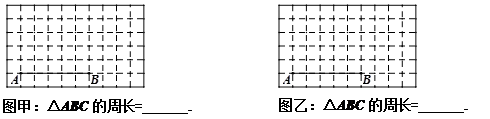
 粤公网安备 44130202000953号
粤公网安备 44130202000953号