（本小题满分12分）
在某海岸A处，发现北偏东
方向，距离A处
n mile的B处有一艘走私船
在A处北偏西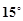
的方向，距离A处
n mile的C处的缉私船奉命以
n mile/h的速度追截走私船. 此时，走私船正以5 n mile/h的速度从B处按照北偏东方向逃窜，问缉私船至少经过多长时间可以追上走私船，并指出缉私船航行方向. 
，设
记
.
的解析表达式；
角是一个三角形的最小内角，试求函数
的值域
(其中
且
,
为实常数)．
，求
的值(用
且
对于
恒成立，求实数m的取值范围(用
且
，求函数
的取值范围．
的定义域；
，求
的最大值与最小值。
，求满足
的实数
的取值范围相关知识点
推荐套卷
（本小题满分12分）
在某海岸A处，发现北偏东方向，距离A处n mile的B处有一艘走私船
在A处北偏西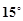的方向，距离A处n mile的C处的缉私船奉命以n mile/h的速度追截走私船. 此时，走私船正以5 n mile/h的速度从B处按照北偏东方向逃窜，问缉私船至少经过多长时间可以追上走私船，并指出缉私船航行方向.
粤公网安备 44130202000953号