(本小题满分12分)热力公司为某生活小区铺设暖气管道,为减 少热量损耗,管道外表需要覆盖保温层。经测算要覆盖可使用20年的保温层,每厘米厚的保温层材料成本为2万元,小区每年的气量损耗用
少热量损耗,管道外表需要覆盖保温层。经测算要覆盖可使用20年的保温层,每厘米厚的保温层材料成本为2万元,小区每年的气量损耗用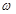 (单位:万元)与保温层厚度
(单位:万元)与保温层厚度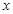 (单位:
(单位: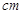 )满足关系:
)满足关系: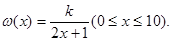 若不加保温层,每年热量损耗费用为5万元。设保温费用与20年的热量损耗费用之和为
若不加保温层,每年热量损耗费用为5万元。设保温费用与20年的热量损耗费用之和为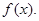
(1)求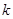 的值及
的值及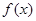 的表达式;
的表达式;
(2)问保温层多厚时,总费用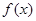 最小,并求最小值。
最小,并求最小值。
推荐套卷
(本小题满分12分)热力公司为某生活小区铺设暖气管道,为减 少热量损耗,管道外表需要覆盖保温层。经测算要覆盖可使用20年的保温层,每厘米厚的保温层材料成本为2万元,小区每年的气量损耗用
少热量损耗,管道外表需要覆盖保温层。经测算要覆盖可使用20年的保温层,每厘米厚的保温层材料成本为2万元,小区每年的气量损耗用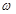 (单位:万元)与保温层厚度
(单位:万元)与保温层厚度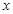 (单位:
(单位: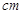 )满足关系:
)满足关系: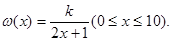 若不加保温层,每年热量损耗费用为5万元。设保温费用与20年的热量损耗费用之和为
若不加保温层,每年热量损耗费用为5万元。设保温费用与20年的热量损耗费用之和为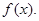
(1)求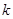 的值及
的值及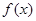 的表达式;
的表达式;
(2)问保温层多厚时,总费用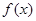 最小,并求最小值。
最小,并求最小值。