(本小题满分12分)已知向量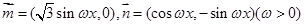 ,在函数
,在函数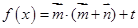 的图像上,对称中心到对称轴的最小距离为
的图像上,对称中心到对称轴的最小距离为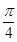 ,且当
,且当 时
时 的最小值为
的最小值为 。
。
(1)求 的解析式;
的解析式;
(2)求 的单调递增区间;
的单调递增区间;
(3)若对任意x1,x2∈[0,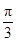 ]都有
]都有 ,求实数
,求实数 m的取值范围。
m的取值范围。
相关知识点
推荐套卷
(本小题满分12分)已知向量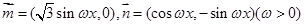 ,在函数
,在函数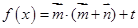 的图像上,对称中心到对称轴的最小距离为
的图像上,对称中心到对称轴的最小距离为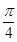 ,且当
,且当 时
时 的最小值为
的最小值为 。
。
(1)求 的解析式;
的解析式;
(2)求 的单调递增区间;
的单调递增区间;
(3)若对任意x1,x2∈[0,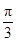 ]都有
]都有 ,求实数
,求实数 m的取值范围。
m的取值范围。