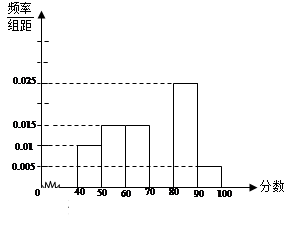
(本小题满分10)某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)...[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)
(3)把90分以上(包括90分)视为成绩优秀,那么从成绩是60分以上(包括60分)的学生中选一人,求此人成绩优秀的概率。
|
相关知识点
推荐套卷
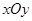 中,直线
中,直线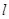 的方程为
的方程为 ,曲线
,曲线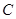 的参数方程为
的参数方程为 (
( 为参数).
为参数). 为极点,以x轴正半轴为极轴)中,点
为极点,以x轴正半轴为极轴)中,点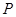 的极坐标为
的极坐标为 ,判断点
,判断点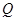 为曲线
为曲线 是圆
是圆 的直径,
的直径, 是圆
是圆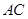 与
与 相交于点
相交于点 ,
,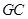 ,
, 是圆
是圆 在
在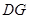 的延长线上,且
的延长线上,且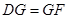 .求证:
.求证: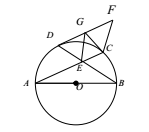
 四点共圆;
四点共圆;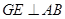 .
. .
. 在点
在点 处的切线与直线x-2=0垂直,求
处的切线与直线x-2=0垂直,求 的单调递减区间和极小值(其中e为自然对数的底数);
的单调递减区间和极小值(其中e为自然对数的底数); ,
, 恒成立,求k的取值范围.
恒成立,求k的取值范围.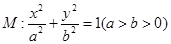 的离心率与双曲线
的离心率与双曲线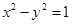 的离心率互为倒数,且椭圆的长轴长为4.
的离心率互为倒数,且椭圆的长轴长为4.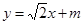 交椭圆M于A,B两点,
交椭圆M于A,B两点, 为椭圆M上一点,求△PAB面积的最大值.
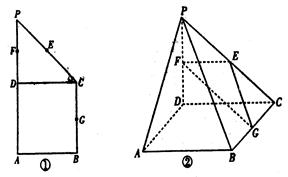
为椭圆M上一点,求△PAB面积的最大值.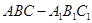 中,侧棱
中,侧棱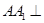 底面ABC,AB⊥BC,D为AC的中点,
底面ABC,AB⊥BC,D为AC的中点, .
.
 平面
平面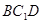 ;
; 的体积.
的体积. 粤公网安备 44130202000953号
粤公网安备 44130202000953号