(本题8分)在平面直角坐标系中,点A的坐标是(1,2).(1)请写出点A关于
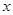 轴的对称点A’和关于
轴的对称点A’和关于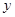 轴的对称点A,,的坐标;
轴的对称点A,,的坐标;(2)在(1)中连结A、 A//,在
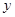 轴上找一点B,使得△ABA//为等边三角形,求出所有满足条件的B坐标;
轴上找一点B,使得△ABA//为等边三角形,求出所有满足条件的B坐标;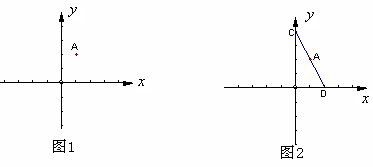
(3)过点A作一条直线交y轴于点C,交x轴于点D,点C的坐标为(0,4),点D的坐标为(2,0)若点P从点D出发,以1个单位每秒的速度向x轴负方向运动;点Q从点C出发,以2个单位每秒的速度向y轴负方向运动,经过多少时间,PQ的长度等于
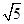 。
。
相关知识点
推荐套卷
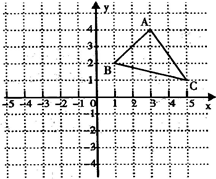
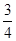 .过点A的另一直线l2:y=-
.过点A的另一直线l2:y=-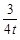 x+b (t>0)与x轴交于点Q,点P是射线AB上的一个动点,过P作PH⊥x轴于点H,设PB=5t.
x+b (t>0)与x轴交于点Q,点P是射线AB上的一个动点,过P作PH⊥x轴于点H,设PB=5t.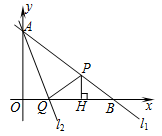
 粤公网安备 44130202000953号
粤公网安备 44130202000953号