.已知双曲线G的中心在原点,它的渐近线与圆x2+y2-10x+20=0相切.过点P(-4,0)作斜率为的直线 ,使得
,使得 和G交于A,B两点,和y轴交于点C,并且点P在线段AB上,又满足|PA|·|PB|=|PC|2.
和G交于A,B两点,和y轴交于点C,并且点P在线段AB上,又满足|PA|·|PB|=|PC|2.
(1)求双曲线G的渐近线的方程;
(2)求双曲线G的方程;
(3)椭圆S的中心在原点,它的短轴是G的实轴.如果S中垂直于 的平行弦的中点的轨迹恰好是G的渐近线截在S内的部分AB,若P(x,y)(y>0)为椭圆上一点,求当
的平行弦的中点的轨迹恰好是G的渐近线截在S内的部分AB,若P(x,y)(y>0)为椭圆上一点,求当 的面积最大时点P的坐标.
的面积最大时点P的坐标.
相关知识点
推荐套卷
 .
. 且
且 ,
, 时,试用含
时,试用含 的式子表示
的式子表示 ,并讨论
,并讨论 的单调区间;
的单调区间; 有零点,
有零点,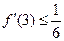 ,且对函数定义域内一切满足
,且对函数定义域内一切满足 的实数
的实数 有
有 .
.  时,求函数
时,求函数 的图象与函数
的图象与函数 的图象的交点坐标
的图象的交点坐标 是圆
是圆 的直径,点
的直径,点 在圆
在圆 ,
,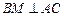 交
交 ,
, 平面
平面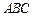 ,
, ,
, .
. ;
; 与平面
与平面
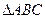 中,角
中,角 的对边分别为
的对边分别为 ,
,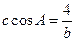 且
且 ,
, 的取值范围;
的取值范围;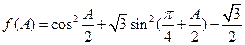 的最值
的最值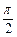 )的图象如图所示,
)的图象如图所示,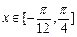 ,求y=f(x)的值域。
,求y=f(x)的值域。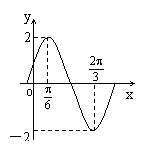
 ,且满足
,且满足
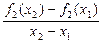 ,a,x1,x2为常数,x1≠x2.
,a,x1,x2为常数,x1≠x2.
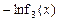 ,x∈(0,e],若F(x)的最小值为6,求实数b的值;
,x∈(0,e],若F(x)的最小值为6,求实数b的值; ,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若
,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若 ,试判断x0,x1,x2的大小,并加以证明.
,试判断x0,x1,x2的大小,并加以证明. 粤公网安备 44130202000953号
粤公网安备 44130202000953号