本题共有3个小题,第1小题满分4分,第2小题满分8分,
第3小题满分6分.
设 把三阶行列式
把三阶行列式 中第一行第二列元素的余子式记为
中第一行第二列元素的余子式记为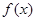 ,且关于
,且关于 的不等式
的不等式 的解集为
的解集为 。各项均为正数的数列
。各项均为正数的数列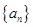 的前
的前 项和为
项和为 ,点列
,点列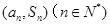 在函数
在函数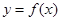 的图象上。
的图象上。
(1)求函数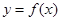 的解析式;
的解析式;
(2)若 ,求
,求 的值;
的值;
(3)令 ,求数列
,求数列 的前
的前 项中满足
项中满足 的所有项数之和.
的所有项数之和.
相关知识点
推荐套卷
本题共有3个小题,第1小题满分4分,第2小题满分8分,
第3小题满分6分.
设 把三阶行列式
把三阶行列式 中第一行第二列元素的余子式记为
中第一行第二列元素的余子式记为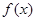 ,且关于
,且关于 的不等式
的不等式 的解集为
的解集为 。各项均为正数的数列
。各项均为正数的数列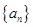 的前
的前 项和为
项和为 ,点列
,点列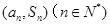 在函数
在函数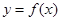 的图象上。
的图象上。
(1)求函数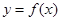 的解析式;
的解析式;
(2)若 ,求
,求 的值;
的值;
(3)令 ,求数列
,求数列 的前
的前 项中满足
项中满足 的所有项数之和.
的所有项数之和.