已知中心在原点，顶点A1、A2在x轴上，离心率e=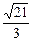
的双曲线过点P(6，6).
(1)求双曲线方程.
(2)动直线l经过△A1PA2的重心G，与双曲线交于不同的两点M、N，问:是否存在直线l,使G平分线段MN，证明你的结论.
相关试题
中，
，
成等比数列数列
的前n项和为Sn，且
.
，求数列
的前
和
．
中，角
，
，
的对边分别为
，且
，求
的值；（2）求sinA＋sinC的最大值.
时，求
的极值
时，求
，恒有
成立，求实数
的取值范围。
，
)，b＝(2，cos2x)．
]，试判断a与b能否平行？
]，求函数f(x)＝a·b的最小值．
和等比数列
中,a1=2b1=2,b6=32,
和
;推荐套卷
已知中心在原点，顶点A1、A2在x轴上，离心率e=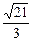的双曲线过点P(6，6).
(1)求双曲线方程.
(2)动直线l经过△A1PA2的重心G，与双曲线交于不同的两点M、N，问:是否存在直线l,使G平分线段MN，证明你的结论.
粤公网安备 44130202000953号