某超市按每袋20元的价格购进某种干果．销售过程中发现，每月销售量y（袋）与销售单价x（元）之间的关系可近似地看作一次函数：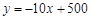
（
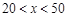）．（1）当x=45元时，y= 袋；当y=200袋时，x= 元；
（2）设这种干果每月获得的利润为w（元），当销售单价定为多少元时，每月 可获得最大利润？最大利润是多少?
倍，购进数量比第一次少了30支．求第一次每支铅笔的进价是多少元？
，且点A、B到原点的距离相等．求x的值．
＝1－
.
＋
＝
.
＋
＝1.相关知识点
推荐套卷
某超市按每袋20元的价格购进某种干果．销售过程中发现，每月销售量y（袋）与销售单价x（元）之间的关系可近似地看作一次函数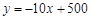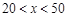：（）．（1）当x=45元时，y= 袋；当y=200袋时，x= 元；
（2）设这种干果每月获得的利润为w（元），当销售单价定为多少元时，每月 可获得最大利润？最大利润是多少?
粤公网安备 44130202000953号