(本小题满分14分)
已知一非零向量列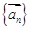 满足:
满足: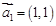 ,
,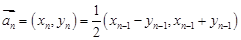
 .
.
(1)证明: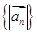 是等比数列;
是等比数列;
(2)设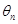 是
是 的夹角
的夹角 ,
,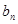 =
=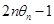 ,
, ,求
,求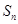 ;
;
(3)设
 ,问数列
,问数列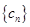 中是否存在最小项?若存在,求出最小值;若不存在,请说明理由.
中是否存在最小项?若存在,求出最小值;若不存在,请说明理由.
相关知识点
推荐套卷
(本小题满分14分)
已知一非零向量列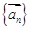 满足:
满足: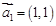 ,
,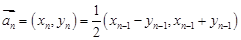
 .
.
(1)证明: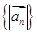 是等比数列;
是等比数列;
(2)设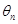 是
是 的夹角
的夹角 ,
,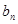 =
=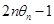 ,
, ,求
,求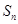 ;
;
(3)设
 ,问数列
,问数列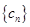 中是否存在最小项?若存在,求出最小值;若不存在,请说明理由.
中是否存在最小项?若存在,求出最小值;若不存在,请说明理由.