（本小题满分12分）
如图，三棱锥P-ABC中，PA⊥底面ABC，AB⊥BC，DE垂直平分PC，且分别交AC、PC于D、E两点，又PB=BC，PA="A" B．
（Ⅰ）求证：PC⊥平面BDE；
（Ⅱ）若点Q是线段PA上任一点，求证：BD⊥DQ；
（Ⅲ）求线段PA上点Q的位置，使得PC//平面BDQ．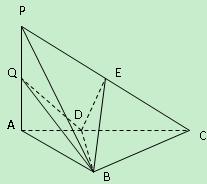
相关试题
:
，命题
: 对任何
R，都有
，命题
的取值范围．
，
，则“
，或
”是“
”的什么条件？
，且
，
，
，使得
在
上为减函数，并且在
上为增函数，若不存在，说明理由.
时，求
.
对任意
,都有
, 
且当
时，都有
.
上单调递减.
.
时，有
,求
的范围.推荐套卷
（本小题满分12分）
如图，三棱锥P-ABC中，PA⊥底面ABC，AB⊥BC，DE垂直平分PC，且分别交AC、PC于D、E两点，又PB=BC，PA="A" B．
（Ⅰ）求证：PC⊥平面BDE；
（Ⅱ）若点Q是线段PA上任一点，求证：BD⊥DQ；
（Ⅲ）求线段PA上点Q的位置，使得PC//平面BDQ．
粤公网安备 44130202000953号