(本小题满分14分)
在平面直角坐标系中,N为圆C: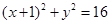 上的一动点,点D(1,0),点M是DN的中点,点P在线段CN上,且
上的一动点,点D(1,0),点M是DN的中点,点P在线段CN上,且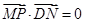 .
.
(Ⅰ)求动点P表示的曲线E的方程;
(Ⅱ)若曲线E与x轴的交点为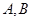 ,当动点P与A,B不重合时,设直线
,当动点P与A,B不重合时,设直线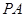 与
与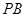 的斜率分别为
的斜率分别为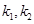 ,证明:
,证明: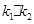 为定值;
为定值;
推荐套卷
(本小题满分14分)
在平面直角坐标系中,N为圆C: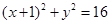 上的一动点,点D(1,0),点M是DN的中点,点P在线段CN上,且
上的一动点,点D(1,0),点M是DN的中点,点P在线段CN上,且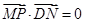 .
.
(Ⅰ)求动点P表示的曲线E的方程;
(Ⅱ)若曲线E与x轴的交点为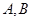 ,当动点P与A,B不重合时,设直线
,当动点P与A,B不重合时,设直线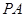 与
与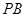 的斜率分别为
的斜率分别为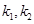 ,证明:
,证明: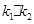 为定值;
为定值;