如图，平面
⊥平面
，四边形与都是直角梯形，∠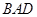
＝∠
＝
，
∥
，
∥
，
、
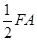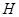分别为
、
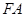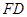的中点．
（Ⅰ）证明：四边形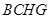
是平行四边形；
（Ⅱ）
、
、
、
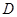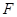四点是否共面？为什么？
(III)设
，证明：平面
⊥平面
.
相关试题
+
+…+
<
.
+
≥a+b.
+lg
+lg
>lga+lgb+lgc.相关知识点
推荐套卷
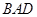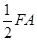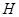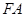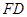如图，平面⊥平面，四边形与都是直角梯形，∠＝∠＝，∥，∥，、分别为、的中点．
（Ⅰ）证明：四边形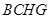是平行四边形；
（Ⅱ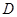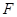）、、、四点是否共面？为什么？
(III)设，证明：平面⊥平面.
粤公网安备 44130202000953号