(本小题满分10分)已知等差数列{an}的首项a1＝1，公差d＞0，且第2项、第5项、第14项分别是一个等比数列的第二项、第三项、第四项．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设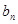
＝
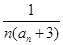（n∈N*），
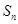＝b1＋b2＋…＋bn，是否存在最大的整数t，使得任意的n均有
总成立？若存在，求出t；若不存在，请说明理由
相关知识点
推荐套卷
(本小题满分10分)已知等差数列{an}的首项a1＝1，公差d＞0，且第2项、第5项、第14项分别是一个等比数列的第二项、第三项、第四项．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设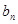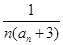＝（n∈N*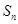），＝b1＋b2＋…＋bn，是否存在最大的整数t，使得任意的n均有总成立？若存在，求出t；若不存在，请说明理由
粤公网安备 44130202000953号