(本题满分16分)
一束光线从点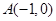
出发，经过直线
上的一点D反射后，经过点
.
⑴求以A,B为焦点且经过点D的椭圆C的方程；
⑵过点作直线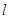
交椭圆C于P、Q两点，以AP、AQ为邻边作平行四边形APRQ,求对角线AR长度的取值范围。
相关试题
中，角
所对的边分别为
，设
为
的大小；（II）若边长
，求
中，
，
的值；（Ⅱ）若
，求
的长．
.
的单调区间；
上的最小值；
，当
时，对任意
，都有
成立，求实数
的取值范围。
的长半轴长为
，且点
在椭圆上．
交椭圆于
两点，若
，求直线推荐套卷
(本题满分16分)
一束光线从点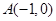出发，经过直线上的一点D反射后，经过点.
⑴求以A,B为焦点且经过点D的椭圆C的方程；
⑵过点作直线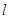交椭圆C于P、Q两点，以AP、AQ为邻边作平行四边形APRQ,求对角线AR长度的取值范围。
粤公网安备 44130202000953号