(10分)(1)如图1，已知点P在正三角形ABC的边BC上，以AP为边作正三角形APQ，连接
CQ．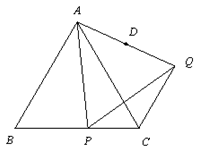
①求证：△ABP≌△ACQ；
②若AB＝6，点D是AQ的中点，直接写出当点P由点B运动到点C时，点D运动路线的
长．(2)已知，△EFG中，EF＝EG＝13，FG＝10．如图2，把△EFG绕点E旋转到△EF＇G＇的位置，点M是边EF＇与边FG的交点，点N在边EG＇上且EN＝EM，连接GN．
求点E到直线GN的距离．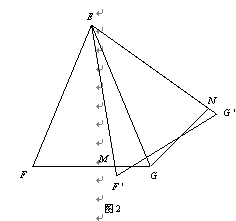
(10分)(1)如图1，已知点P在正三角形ABC的边BC上，以AP为边作正三角形APQ，连接
CQ．
①求证：△ABP≌△ACQ；
②若AB＝6，点D是AQ的中点，直接写出当点P由点B运动到点C时，点D运动路线的
长．(2)已知，△EFG中，EF＝EG＝13，FG＝10．如图2，把△EFG绕点E旋转到△EF＇G＇的位置，点M是边EF＇与边FG的交点，点N在边EG＇上且EN＝EM，连接GN．
求点E到直线GN的距离．
，
，
的方程组
的解满足不等式
,求实数
的取值范围。
并把解集在数轴上表示.
的所有自然数解
粤公网安备 44130202000953号