如图,抛物线y=ax2+bx+c经过点A( 0,4)、B(2,4),它的最高点纵坐标为
0,4)、B(2,4),它的最高点纵坐标为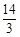 ,点P是第一象限抛物线上一点且PA=PO,过点P的直线分别交射线AB、x正半轴于C、D.设AC=m,OD=n.
,点P是第一象限抛物线上一点且PA=PO,过点P的直线分别交射线AB、x正半轴于C、D.设AC=m,OD=n.
(1)求此抛物线的解析式;
(2)求点P的坐标及n关于m的函数关系式;
(3)连结OC交AP于点E,如果以A、C、E为顶点的三角形与△ODP相似,求m的值.
相关知识点
推荐套卷
如图,抛物线y=ax2+bx+c经过点A( 0,4)、B(2,4),它的最高点纵坐标为
0,4)、B(2,4),它的最高点纵坐标为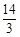 ,点P是第一象限抛物线上一点且PA=PO,过点P的直线分别交射线AB、x正半轴于C、D.设AC=m,OD=n.
,点P是第一象限抛物线上一点且PA=PO,过点P的直线分别交射线AB、x正半轴于C、D.设AC=m,OD=n.
(1)求此抛物线的解析式;
(2)求点P的坐标及n关于m的函数关系式;
(3)连结OC交AP于点E,如果以A、C、E为顶点的三角形与△ODP相似,求m的值.