已知等比数列{xn}的各项为不等于1的正数,数列{yn}满足 =2(a>0,且a≠1),设y3="18," y6=12.
=2(a>0,且a≠1),设y3="18," y6=12.
(1)数列{yn}的前多少项和最大,最大值为多少?
(2)试判断是否存在自然数M,使得当n>M时,xn>1恒成立,若存在,求出相应的M;若不存在,请说明理由;
(3)令
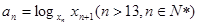 试比较
试比较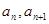 的大小.
的大小.
相关知识点
推荐套卷
已知等比数列{xn}的各项为不等于1的正数,数列{yn}满足 =2(a>0,且a≠1),设y3="18," y6=12.
=2(a>0,且a≠1),设y3="18," y6=12.
(1)数列{yn}的前多少项和最大,最大值为多少?
(2)试判断是否存在自然数M,使得当n>M时,xn>1恒成立,若存在,求出相应的M;若不存在,请说明理由;
(3)令
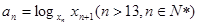 试比较
试比较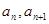 的大小.
的大小.