如图，F1，F2是离心率为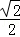
的椭圆C：
（a＞b＞0）的左、右焦点，直线l：x=﹣
将线段F1F2分成两段，其长度之比为1：3．设A，B是C上的两个动点，线段AB的中垂线与C交于P，Q两点，线段AB的中点M在直线l上．
（1）求椭圆C的方程；
（2）求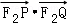
的取值范围．
相关试题
的最小值。推荐套卷
如图，F1，F2是离心率为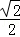的椭圆C：（a＞b＞0）的左、右焦点，直线l：x=﹣将线段F1F2分成两段，其长度之比为1：3．设A，B是C上的两个动点，线段AB的中垂线与C交于P，Q两点，线段AB的中点M在直线l上．
（1）求椭圆C的方程；
（2）求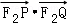的取值范围．
粤公网安备 44130202000953号