如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB。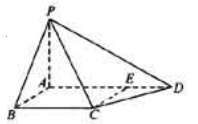
（1）求证：CE⊥平面PAD；
（2）若PA=AB=1，AD=3，CD=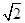 
，∠CDA=45°，求四棱锥P-ABCD的体积
的值．
，当
时，有
，
的值，使
与
都是有限的．相关知识点
推荐套卷
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB。
（1）求证：CE⊥平面PAD；
（2）若PA=AB=1，AD=3，CD= 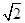，∠CDA=45°，求四棱锥P-ABCD的体积
粤公网安备 44130202000953号