如图，在平面直角坐标系中，△ABC的三个顶点
坐标分别是A（2，3）、B（2，1）、C（3，2）．
① 判断△ABC的形状；②如果将△ABC沿着边AC旋转，求所得旋转体的全面积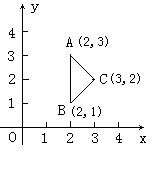
如图，方格纸中有三个点A，B，C，要求作一个四边形使这三个点在这个四边形的边（包括顶点）上，且四边形的顶点在方格的格点上．
①在图甲中作出的四边形是中心对称图形但不是轴对称图形；
②在图乙中作出的四边形是轴对称图形但不是中心对称图形；
③在图丙中作出的四边形既是轴对称图形又是中心对称图形．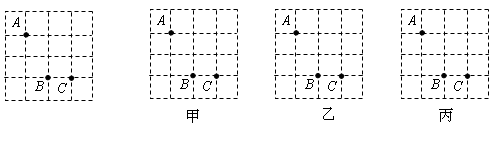
相关试题
如图，给出五个等量关系：①AD=BC；②AC=BD；③CE=DE；④∠D=∠C；⑤∠DAB=∠CBA．请你以其中两个为条件，另三个中的一个为结论，推出一个正确的结论（只需写出一种情况），并加以证明．
；
相关知识点
推荐套卷
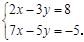
粤公网安备 44130202000953号