将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表:
a1
a2 a3
a4 a5 a6
a7 a8 a9 a10
……
记表中的第一列数a1,a2,a4,a7,…构成的数列为{bn},b1=a1="1." Sn为数列{bn}的前n项和,且满足 =1(n≥2).
=1(n≥2).
(Ⅰ)证明数列{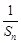 }成等差数列,并求数列{bn}的通项公式;
}成等差数列,并求数列{bn}的通项公式;
(Ⅱ)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当 时,求上表中第k(k≥3)行所有项的和.
时,求上表中第k(k≥3)行所有项的和.
推荐套卷
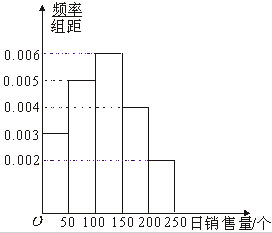
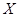 表示在未来3天里日销售量不低于100个的天数,求随机变量
表示在未来3天里日销售量不低于100个的天数,求随机变量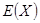 及方差
及方差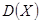 .
.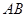 是圆
是圆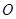 的直径,
的直径,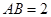 ,
,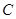 是⊙
是⊙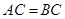 ,
,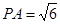 ,
,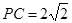 ,
,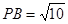
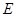 是
是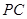 的中点,
的中点,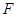 是
是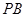 的中点
的中点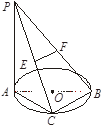
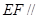 平面
平面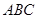 ;
;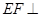 平面
平面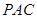 ;
; ,其中常数
,其中常数 .
. 时,求函数
时,求函数 的极值点;
的极值点; 恒成立;
恒成立; 图象上的不同两点
图象上的不同两点 ,如果在函数
,如果在函数 (其中
(其中 ),使得在点M处的切线
),使得在点M处的切线 ∥AB,则称直线AB存在“伴侣切线”.特别地,当
∥AB,则称直线AB存在“伴侣切线”.特别地,当 ,又称直线AB存在“中值伴侣切线”.
,又称直线AB存在“中值伴侣切线”. 时,对于函数
时,对于函数 :
: (
( )的长半轴长为2,离心率为
)的长半轴长为2,离心率为 ,左右焦点分别为
,左右焦点分别为 ,
, .
.
 与椭圆
与椭圆 ,
, 两点,与以
两点,与以 ,
, 为直径的圆交于
为直径的圆交于 ,
, 两点,且满足
两点,且满足 ,求直线
,求直线 的方程.
的方程. 粤公网安备 44130202000953号
粤公网安备 44130202000953号