(本小题满分14分)已知函数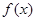 定义在区间
定义在区间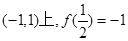 ,对任意
,对任意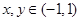 ,恒有
,恒有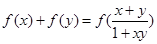 成立,又数列
成立,又数列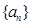 满足
满足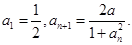 (I)在(-1,1)内求一个实数t,使得
(I)在(-1,1)内求一个实数t,使得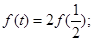 (II)求证:数列
(II)求证:数列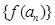 是等比数列,并求
是等比数列,并求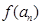 的表达式;(III)设
的表达式;(III)设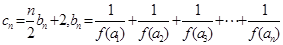 ,是否存在
,是否存在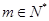 ,使得对任意
,使得对任意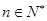 ,
,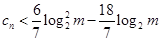 恒成立?若存在,求出m的最小值;若不存在,请说明理由。
恒成立?若存在,求出m的最小值;若不存在,请说明理由。
推荐套卷
(本小题满分14分)已知函数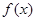 定义在区间
定义在区间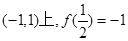 ,对任意
,对任意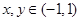 ,恒有
,恒有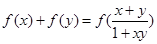 成立,又数列
成立,又数列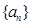 满足
满足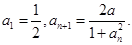 (I)在(-1,1)内求一个实数t,使得
(I)在(-1,1)内求一个实数t,使得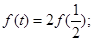 (II)求证:数列
(II)求证:数列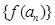 是等比数列,并求
是等比数列,并求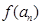 的表达式;(III)设
的表达式;(III)设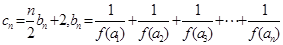 ,是否存在
,是否存在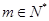 ,使得对任意
,使得对任意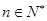 ,
,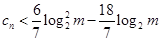 恒成立?若存在,求出m的最小值;若不存在,请说明理由。
恒成立?若存在,求出m的最小值;若不存在,请说明理由。