某风景区的湖心岛靠水边有一凉亭A，其正东方向的湖边B处有一棵大树，游客李先生必须在10分钟之内从湖心岛凉亭A处划船赶回湖边B，否则
他将赶不上旅游车约定的发车时间．已知湖边建筑物C在凉亭A的南偏东45°方向上，也在大树B的南偏西32°的方向上，且量得B、C间的距离为100m．若
李先生立即登船以15m/s的速度划行，问他能否在规定时间内赶到B处？
(参考数据：sin32°＝0.5299 cos32°＝0.8480)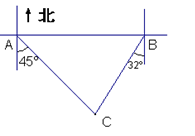
相关试题
，化简 
再求值．
,（2）
已知：如图1，M是定长线段AB上一定点，C、D两点分别从M、B出发以1cm/s、3 cm/s的速度沿直线BA向左运动，运动方向如箭头所示（C在线段AM上，D在线段BM上）
（1）若AB=10cm,当点C、D运动了2s，求AC+MD的值．
（2）若点C、D运动时， 总有MD＝3AC，直接填空:AM= AB．
（3）在（2）的条件下，N是直线AB上一点，且AN－BN=MN，求
的值．
且x与y互为相反数，y 与z 为倒数．相关知识点
推荐套卷
粤公网安备 44130202000953号