在平面直角坐标系xOy中,二次函数y=mx2+(m-3)x-3(m>0)的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.

求点A的坐标;
当∠ABC=45°时,求m的值;
已知一次函数y=kx+b,点P(n,0)是x轴上的一个动点,在(2)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数y=mx2+(m-3)x-3(m>0)的图象于点N.若只有当-2<n<2时,点M位于点N的上方,求这个一次函数的解析式.(友情提示:自画图形)
相关知识点
推荐套卷
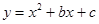 中,函数
中,函数 与自变量
与自变量 的部分对应值如下表:
的部分对应值如下表: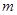 ,
, ),B(
),B(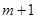 ,
, )都在该抛物线上,试比较y1和y2的大小.
)都在该抛物线上,试比较y1和y2的大小. .
. 轴一定有两个交点;
轴一定有两个交点;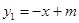 与二次函数
与二次函数 的图象上.
的图象上.
 和
和 ,
,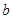 的值;
的值; >
> 时,自变量
时,自变量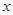 的取值范围.
的取值范围.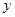 轴正半轴上,且AB=OC.
轴正半轴上,且AB=OC.
 与
与 轴交点的横坐标分别为-1和2,且经过点(3,8),求这个抛物线的解析式.
轴交点的横坐标分别为-1和2,且经过点(3,8),求这个抛物线的解析式. 粤公网安备 44130202000953号
粤公网安备 44130202000953号