已知二次函数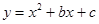 中,函数
中,函数 与自变量
与自变量 的部分对应值如下表:
的部分对应值如下表:
 |
… |
-1 |
0 |
1 |
2 |
3 |
4 |
… |
 |
… |
10 |
5 |
2 |
1 |
2 |
5 |
… |
(1)求该二次函数的解析式;
(2)当 为何值时,
为何值时, 有最小值?最小值是多少?
有最小值?最小值是多少?
(3)若A(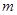 ,
, ),B(
),B(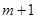 ,
, )都在该抛物线上,试比较y1和y2的大小.
)都在该抛物线上,试比较y1和y2的大小.
相关知识点
推荐套卷
 为
为 的切线,
的切线, 为切点,
为切点, 交
交 ,求
,求 的度数.
的度数.


 表,可从图表中得出:我国
表,可从图表中得出:我国 经济发展过热的最高点出现在 年;我国经济发展过冷的最低点出现在 年.
经济发展过热的最高点出现在 年;我国经济发展过冷的最低点出现在 年.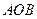 中,
中,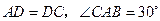 ,
,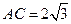 ,求
,求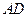 的长度.
的长度.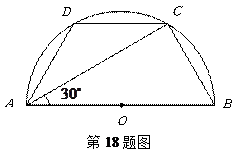
 拟台球游戏,为简单起见,约定:①每个球袋视为一个点,如果不遇到障碍,各球均沿直线前进;②A球击B球,意味着B球在A球前进的路线上,且B球被撞击后沿A球原来的方向前进;③球撞击桌边后的反弹角度等于入射角度,(如图中∠β=∠a)如图所示,设桌边只剩下白球,A,6号球B。
拟台球游戏,为简单起见,约定:①每个球袋视为一个点,如果不遇到障碍,各球均沿直线前进;②A球击B球,意味着B球在A球前进的路线上,且B球被撞击后沿A球原来的方向前进;③球撞击桌边后的反弹角度等于入射角度,(如图中∠β=∠a)如图所示,设桌边只剩下白球,A,6号球B。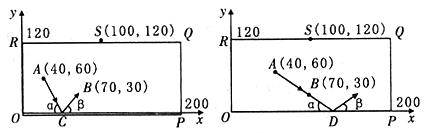
 粤公网安备 44130202000953号
粤公网安备 44130202000953号