汽车和自行车分别从A地和C地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米。(汽车开到C地即停止)
(1)经过 秒后,汽车到达B处,自行车到达D处,设B、D间距离为
秒后,汽车到达B处,自行车到达D处,设B、D间距离为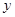 ,写出
,写出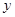 关于
关于 的函数关系式,并求出定义域。
的函数关系式,并求出定义域。
(2)经过多少时间后,汽车和自行车之间的距离最短?最短距离是多少?
推荐套卷
汽车和自行车分别从A地和C地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米。(汽车开到C地即停止)
(1)经过 秒后,汽车到达B处,自行车到达D处,设B、D间距离为
秒后,汽车到达B处,自行车到达D处,设B、D间距离为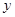 ,写出
,写出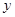 关于
关于 的函数关系式,并求出定义域。
的函数关系式,并求出定义域。
(2)经过多少时间后,汽车和自行车之间的距离最短?最短距离是多少?