一次远足，小明与小聪分别从A，B两个景点出发，沿同一条公路相向而行。他们出发的时间是上午8：00，小聪行走的速度是小明的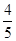
， A，B两个景点之间的路程是9千米.设小明行走的速度为x千米/小时.经过t小时，在小明和小聪相遇前，他们相距多少千米？
如果小聪行走的速度是4千米/小时，那么到几时几分，小明与小聪相距3千米？
，
，
，求
的值.
， （2）
与
是同类项.求代数式：
的值.
的2倍得
，求这个多项式
，其中
，
。
相关知识点
推荐套卷
一次远足，小明与小聪分别从A，B两个景点出发，沿同一条公路相向而行。他们出发的时间是上午8：00，小聪行走的速度是小明的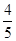， A，B两个景点之间的路程是9千米.设小明行走的速度为x千米/小时.经过t小时，在小明和小聪相遇前，他们相距多少千米？
如果小聪行走的速度是4千米/小时，那么到几时几分，小明与小聪相距3千米？
粤公网安备 44130202000953号