如图,在Rt△ABC中,∠ACB=90º,AB=10,AC=6 ,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
(1)当AD=3时,求DE的长;
(2)当点
 E、F在边AC、BC上移动时,设
E、F在边AC、BC上移动时,设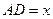 ,
, ,
,
求 关于
关于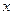 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(3)在点E、F移动过
 程中,△AED与△CEF能否相似,
程中,△AED与△CEF能否相似,
若能,求AD的长;若不能,请说明理由.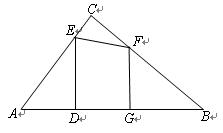
相关知识点
推荐套卷
如图,在Rt△ABC中,∠ACB=90º,AB=10,AC=6 ,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
(1)当AD=3时,求DE的长;
(2)当点
 E、F在边AC、BC上移动时,设
E、F在边AC、BC上移动时,设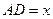 ,
, ,
,
求 关于
关于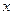 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(3)在点E、F移动过
 程中,△AED与△CEF能否相似,
程中,△AED与△CEF能否相似,
若能,求AD的长;若不能,请说明理由.