(本题满分13分)
已知函数
在
上是减函数，在
上是增函数，函数
在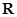
上有三个零点．
（1）求
的值；
（2）若1是其中一个零点，求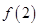
的取值范围；
（3）若
，试问过点（2，5）可作多少条直线与曲线y=g(x)相切？请说明理由。
相关试题
在点
处取得极大值
，其导函数
的图象经过点
，
，如图所示.求：
的值.（05北京卷）已知函数f(x)=－x3＋3x2＋9x＋a,
（I）求f(x)的单调递减区间；
（II）若f(x)在区间[－2，2]上的最大值为20，求它在该区间上的最小值．
通过点
，且在
处的切线方程为
，求
表达式。
且与曲线
相切的直线方程。
是曲线
上任意一点，求点
的最小距离。推荐套卷
(本题满分13分)
已知函数在上是减函数，在上是增函数，函数在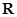上有三个零点．
（1）求的值；
（2）若1是其中一个零点，求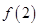的取值范围；
（3）若，试问过点（2，5）可作多少条直线与曲线y=g(x)相切？请说明理由。
（05北京卷）已知函数f(x)=－x3＋3x2＋9x＋a,
（I）求f(x)的单调递减区间；
（II）若f(x)在区间[－2，2]上的最大值为20，求它在该区间上的最小值．
粤公网安备 44130202000953号