(本小题满分15分)如果数列 同时满足以下两个条件:(1)各项均不为0;(2)存在常数
同时满足以下两个条件:(1)各项均不为0;(2)存在常数 ,
,
对任意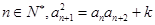 都成立,则称这样的数列
都成立,则称这样的数列 为“
为“ 类等比数列”.
类等比数列”.
(Ⅰ)若数列 满足
满足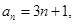 证明数列
证明数列 为“
为“ 类等比数列”,并求出相应的
类等比数列”,并求出相应的 的值;
的值;
(Ⅱ)若数列 为“
为“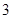 类等比数列”,且满足
类等比数列”,且满足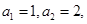 问是否存在常数
问是否存在常数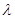 ,使得
,使得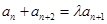 对
对
任意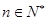 都成立?若存在,求出
都成立?若存在,求出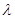 ,若不存在,请举出反例.
,若不存在,请举出反例.
相关知识点
推荐套卷
(本小题满分15分)如果数列 同时满足以下两个条件:(1)各项均不为0;(2)存在常数
同时满足以下两个条件:(1)各项均不为0;(2)存在常数 ,
,
对任意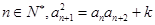 都成立,则称这样的数列
都成立,则称这样的数列 为“
为“ 类等比数列”.
类等比数列”.
(Ⅰ)若数列 满足
满足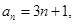 证明数列
证明数列 为“
为“ 类等比数列”,并求出相应的
类等比数列”,并求出相应的 的值;
的值;
(Ⅱ)若数列 为“
为“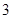 类等比数列”,且满足
类等比数列”,且满足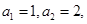 问是否存在常数
问是否存在常数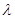 ,使得
,使得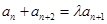 对
对
任意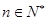 都成立?若存在,求出
都成立?若存在,求出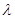 ,若不存在,请举出反例.
,若不存在,请举出反例.