(本题满分15分)四棱锥P－ABCD中，PA⊥平面ABCD，E为AD的中点，ABCE为菱形，∠BAD＝120°，PA＝AB，G，F分别是线段CE，PB上的动点，且满足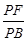
＝
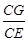＝λ∈(0，1)．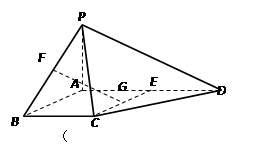
(Ⅰ) 求证：FG∥平面PDC；
(Ⅱ) 求λ的值，使得二面角F－CD－G的平面角的正切值为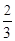
．
相关试题
的图象与x轴的交点中，相邻两个交点之间的距离为
，且图象上一个最高点
的解析式；
的前6项和为60，且
的等比中项
满足：
，求数列
的值；
的值。
满足：
的值，猜测
的表达式并给予证明；
的前n项和为
的图象上移动时，点
的图象上移动。
的图象上，求t的值；
的解析式；
的解集是
，求实数t的取值范围。推荐套卷
(本题满分15分)四棱锥P－ABCD中，PA⊥平面ABCD，E为AD的中点，ABCE为菱形，∠BAD＝120°，PA＝AB，G，F分别是线段CE，PB上的动点，且满足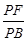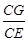＝＝λ∈(0，1)．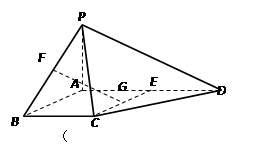
(Ⅰ) 求证：FG∥平面PDC；
(Ⅱ) 求λ的值，使得二面角F－CD－G的平面角的正切值为．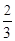
粤公网安备 44130202000953号