有一种密英文的明文(真实文)按字母分解,其中英文的a,b,c,…,z的26个字母(不分大小写),依次对应1,2,3,…,26这26个自然数,见如下表格:
a
|
b
|
c
|
d
|
e
|
f
|
g
|
h
|
i
|
j
|
k
|
l
|
m
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
n
|
o
|
p
|
q
|
r
|
s
|
t
|
u
|
v
|
w
|
x
|
y
|
z
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
26
|
给出如下变换公式:

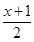 (x∈N,1≤x≤26,x不能被2整除)
(x∈N,1≤x≤26,x不能被2整除)
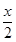 +13(x∈N,1≤x≤26,x能被2整除)
+13(x∈N,1≤x≤26,x能被2整除)
将明文转换成密文,如8→ +13=17,即h变成q;如5→
+13=17,即h变成q;如5→ =3,即e变成c.
=3,即e变成c.
①按上述规定,将明文good译成的密文是什么?
②按上述规定,若将某明文译成的密文是shxc,那么原来的明文是什么?