如图,在棱长为1的正方体 中, ,截面 .
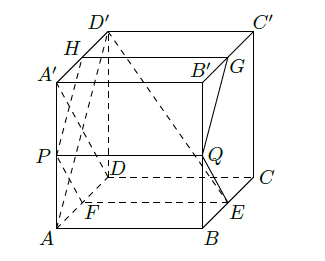
(Ⅰ)证明:平面
和平面
互相垂直;
(Ⅱ)证明:截面
和截面
面积之和是定值,
并求出这个值;
(Ⅲ)若
,求
与平面
所成角的正弦值.
推荐套卷
如图,在棱长为1的正方体 中, ,截面 .

(Ⅰ)证明:平面
和平面
互相垂直;
(Ⅱ)证明:截面
和截面
面积之和是定值,
并求出这个值;
(Ⅲ)若
,求
与平面
所成角的正弦值.