(本小题12分)提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度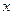 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当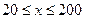 时,车流速度v是车流密度
时,车流速度v是车流密度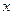 的一次函数.
的一次函数.
(Ⅰ)当 时,求函数
时,求函数 的表达式;
的表达式;
(Ⅱ)当车流密度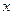 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时)
可以达到最大,并求出最大值(精确到1辆/小时)
推荐套卷
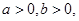 且
且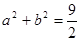 ,若
,若 恒成立,
恒成立,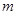 的最小值;
的最小值;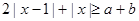 对任意的
对任意的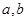 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 中,直线
中,直线 的方程为
的方程为 ,曲线
,曲线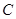 的参数方程为
的参数方程为 .
.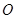 为极点,以
为极点,以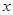 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点 的极坐标为
的极坐标为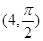 ,判断点
,判断点 是曲线
是曲线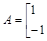
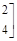 .
. 的逆矩阵
的逆矩阵 ;
;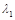 、
、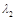 和对应的一个特征向量
和对应的一个特征向量 、
、 .
. 的导函数是
的导函数是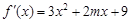 ,
, 处取得极值,且
处取得极值,且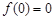 ,
, 上的最大值为
上的最大值为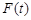 ,若对任意的
,若对任意的
 总有
总有 成立,求
成立,求 的取值范围;
的取值范围;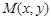 是曲线
是曲线 上的任意一点.当
上的任意一点.当 时,求直线OM斜率的最小值,据此判断
时,求直线OM斜率的最小值,据此判断 的大小关系,并说明理由.
的大小关系,并说明理由.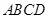 是原棚户建筑用地,测量可知边界
是原棚户建筑用地,测量可知边界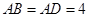 万米,
万米,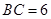 万米,
万米,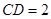 万米.
万米.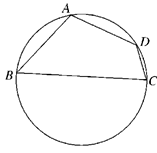
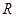 的值;
的值; 、
、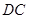 不能变更,而边界
不能变更,而边界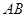 、
、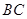 可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧
可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧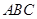 上设计一点
上设计一点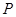 ;使得棚户区改造的新建筑用地
;使得棚户区改造的新建筑用地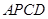 的面积最大,并求最大值.
的面积最大,并求最大值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号