(本题满分15分)抛物线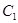 的方程是
的方程是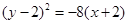 ,曲线
,曲线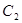 与
与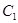 关于点
关于点 对称.(Ⅰ)求曲线
对称.(Ⅰ)求曲线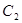 的方程; (Ⅱ)过点(8,0)的直线
的方程; (Ⅱ)过点(8,0)的直线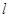 交曲线
交曲线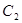 于M、N两点,问在坐标平面上能否找到某个定点
于M、N两点,问在坐标平面上能否找到某个定点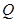 ,不论直线
,不论直线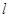 如何变化,总有
如何变化,总有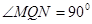 。若找不到,请说明理由;若能找到,写出满足要求的所有的点
。若找不到,请说明理由;若能找到,写出满足要求的所有的点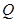 的坐标.
的坐标.
推荐套卷
(本题满分15分)抛物线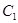 的方程是
的方程是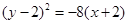 ,曲线
,曲线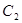 与
与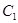 关于点
关于点 对称.(Ⅰ)求曲线
对称.(Ⅰ)求曲线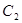 的方程; (Ⅱ)过点(8,0)的直线
的方程; (Ⅱ)过点(8,0)的直线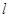 交曲线
交曲线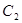 于M、N两点,问在坐标平面上能否找到某个定点
于M、N两点,问在坐标平面上能否找到某个定点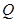 ,不论直线
,不论直线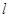 如何变化,总有
如何变化,总有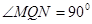 。若找不到,请说明理由;若能找到,写出满足要求的所有的点
。若找不到,请说明理由;若能找到,写出满足要求的所有的点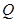 的坐标.
的坐标.