(本小题满分14分)
已 知二次函数
知二次函数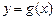 的图象经过点
的图象经过点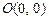 、
、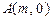 与点
与点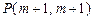 ,设函数
,设函数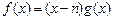 在
在 和
和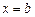 处取到极值,其中
处取到极值,其中 ,
,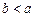 。
。
(1)求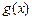 的二次项系数
的二次项系数 的值;
的值;
(2)比较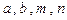 的大小(要求按从小到大排列);
的大小(要求按从小到大排列);
(3)若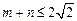 ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线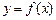 均相切,求
均相切,求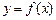 。
。
相关知识点
推荐套卷
(本小题满分14分)
已 知二次函数
知二次函数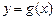 的图象经过点
的图象经过点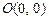 、
、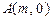 与点
与点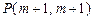 ,设函数
,设函数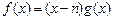 在
在 和
和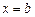 处取到极值,其中
处取到极值,其中 ,
,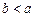 。
。
(1)求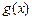 的二次项系数
的二次项系数 的值;
的值;
(2)比较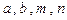 的大小(要求按从小到大排列);
的大小(要求按从小到大排列);
(3)若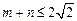 ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线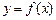 均相切,求
均相切,求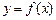 。
。